Verhoudingen en breuken

Je zal opgaven tegenkomen waarin zowel breuken als verhoudingen verwerkt zij. Om dit te kunnen oplossen maak je weer gebruik van verhoudingstabellen. Hierdoor houd je overzicht en weet je wat je exact moet doen.

Werken met breuken heb je al eerder gedaan. Mocht je dit deel niet meer beheersen, raad ik je aan om toch even terug in de tijd te gaan. Bestudeer nog eens kort wat breuken ook alweer waren, en onthoud:

Een breuk is ook een verhouding!

1/3 is hetzelfde als 2/6! Ik kan zelfs hier een verhoudingstabel toepassen, kijk maar.

Stel dat 2 op 5 studenten een spijkerbroek dragen. Daar zit ook weer een breuk verstopt. Namelijk 2/5.

Als je dit in een tabel plaatst ziet dat er zo uit:

Je ziet het, een breuk en een verhouding zijn precies hetzelfde. Ze laten beiden zien dat er een deel van het totaal is , en een totaal zelf.

Net als bij breuken heb je een teller en noemer.

7.1 Verhoudingen met een totaal

Hiernaast zie je een pot met heerlijke Mexicaanse guacamole, met echte avocado er in verwerkt.

Vraag: Hoeveelste deel is de avocado ten opzichte van de hele pot?

Er zit 250 gram in de pot, en 50 gram daarvan is avocado.

Dus 50/250 is avocado Máár .... breuken moet je vereenvoudigen, weet je nog?

Wanneer ik deze breuk in een verhoudingstabel plaats zie je dat ik hem op een gemakkelijke wijze kan vereenvoudigen. Ik deel de teller en de noemer beide door 50.

Kijk maar eens hiernaast.

Dit betekent dus 1 deel van de 5 delen van de guacamole uit avocado bestaat. (1/5 deel)

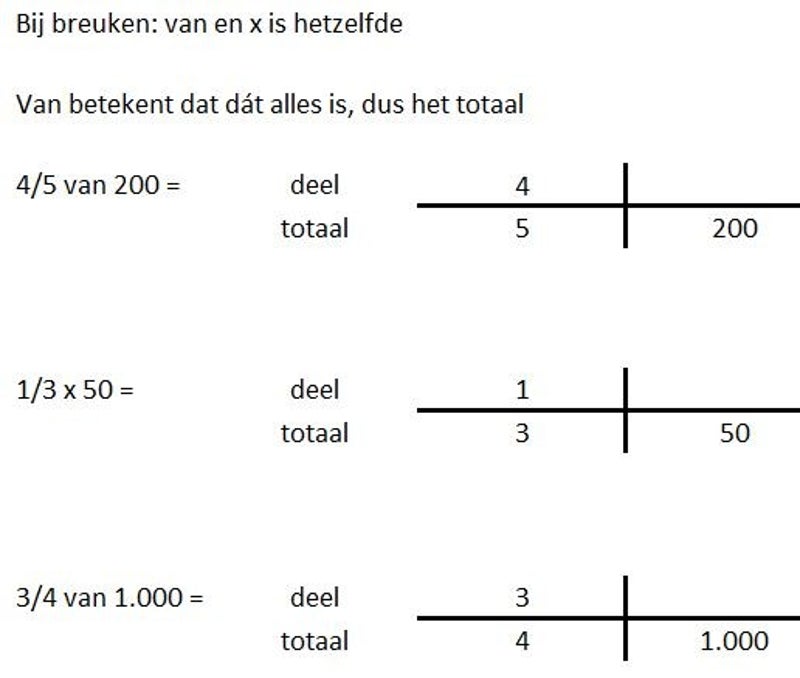
Even handig om te weten:

Bij het rekenen met breuken betekenen x en van hetzelfde!

Kijk hiernaast maar.

7.2 Rekenen met verhoudingen

Hier een som waarbij je aan de hand van een breuk een totaal moet uitrekenen.

Zolang je gebruik maakt van het verhoudingstabel moet het je lukken om dit soort sommen te maken.

Ik maak weer een verhoudingstabel, en vul in waar het over gaat. We hebben een deel en een totaal. 1 is dus het deel van de foto's en de 3 is het totaal aantal foto's.

Ik weet dat 43 foto's 1 van de 3 delen is, dus komt de 43 naast de 1 te staan in het tabel.

Nu ik dit weet kan ik aan de slag: 3 : 1 x 43 = 129 foto's.

In totaal zijn er dus 129 foto's gemaakt.

Belangrijk om te begrijpen is dat er 43 foto's gemaakt zijn. Dat zijn niet alle foto's, maar slechts 1/3.

We moeten hier dus uitrekenen hoeveel alle foto's samen zijn, dus 3/3.

Hier enkele vragen om te oefen waarbij je moet kijken welk getal waar bijhoort. Hoort het bij de teller of bij de noemer?

Almelo heeft 70.000 inwoners. 3 op de 8 heeft een auto. Hoeveel auto’s zijn er in Almelo?

Vraag: Hoort de 70.00 bij de teller (3), of hoort het bij de noemer (8)?

De 70.000 hoort bij de noemer (8), want dit zijn het totaal aantal inwoners van Almelo. Ik moet hier dus een deel uitrekenen, en daar komt dan ook mijn vraagteken te staan in het tabel.

Als ik hier nu ook een tabel bij maak, dan ziet deze er zo uit:

Pino maakt een zeiltocht met zijn boot. Hij heeft al 360 km gevaren. Dat is 2/3 van zijn totale tocht. Wat is de totale lengte van zijn tocht?

Vraag: Waar hoort de 360 bij? Hoort deze bij de teller (2) of bij de noemer (3)?

De 360 hoort bij de teller, want in de opgave staat letterlijk dat de 360 km 2 van de 3 is. Daarnaast staat er verder te lezen dat er gevraagd wordt naar de totale lengte. Ik moet hier dus het totaal uitrekenen, en plaats daar dan ook het vraagteken in het tabel.

In een tabel ziet dat er zo uit:

Toegepast rekenen

Bij toegepast rekenen is het heel erg belangrijk dat je erg nauwkeurig leest wat er in de tekst staan, maar ook goed de eventuele plaatjes bestudeerd. Welke informatie is daarin te vinden, en wat is van belang voor jou?

De organisatie van het kinderkamp heeft voor de eerste week van de vakantie 18 begeleiders die mee op kamp kunnen.

Vraag: Hoeveel kinderen kunnen er die week maximaal mee op kamp?

Ik maak dus een verhoudingstabel en noteer eerst waar het over gaat. In dit geval gaat het om begeleiders en kinderen. Het maakt niet uit of je de kinderen boven of onder plaatst, maar noteer de benaming wel, zodat je de juiste getallen op juiste plaats zet.

De 18 (het aantal begeleiders) hoort dus bij de 3 te staan, en ik moet uitrekenen hoeveel kinderen er dan mee kunnen, dus daar plaats ik mijn vraagteken.

Nu ik het tabel zover mogelijk heb ingevuld kan ik de berekening maken zoals we dat altijd doen. We starten met het getal naast het vraagteken etc.

Kijk hiernaast maar. Er kunnen maximaal 120 kinderen mee.

In de meubelfabriek werken zijn er 96 werknemers, waarvan 32 vrouw zijn.

Bij de ijscofabriek werken 140 werknemers, waarvan 2/5 vrouw zijn.

In welke fabriek werken naar verhouding de meeste vrouwen?

En waar werken daadwerkelijk de meeste vrouwen?

We rekenen eerst uit wat de verhouding man/vrouw is bij de meubelfabriek. Deze heeft heeft 96 werknemers, waarvan 32 vrouwen. Dit vul ik in in mijn verhoudingstabel. Ik moet nu uitrekenen wat de verhouding is

Ik start met het getal naast mijn ?.

Ik steek over en deel, dan opzij en vermenigvuldigen.

96 : 32 x 1 = 3

Dat komt dus neer op een verhouding van 1 vrouw op 3 werknemers.

vrouwen 1 : 3 totaal

Bij de ijscofabriek werken 140 werknemers, waarvan 2/5 vrouw is.

Ook hier vul ik nu weer een verhoudingstabel in.

Ik start met het getal naast mijn ?.

Ik steek over en deel, dan opzij en vermenigvuldigen.

2 : 5 x 140 = 56

Er werken dus 56 vrouwen bij de ijscofabriek.

We weten nu dat er bij de meubelfabriek 32 vrouwen werken en 56 bij de ijscofabriek.

Maar wat zijn nu de verhoudingen ten opzichte van elkaar? Wat is meer, 1/3 of 2/5?

Om dat te weten te komen moeten we zorgen dat de noemers hetzelfde worden.

Net als bij breuken gaan we de noemers gelijk maken door deze met elkaar te gaan vermenigvuldigen, en komen we op een gezamenlijke noemer van 15. Kijk hieronder maar.

Hiernaast zie je dat bij de meubelfabriek de verhouding 5 : 15 is, en bij de ijscofabriek is het 6 : 15. Bij de ijscofabriek werken dus meer vrouwen.