Kaart en

schaal

Windrichtingen

Om een route te kunnen lopen met behulp van een kaart is het van belang dat je je kunt oriënteren op de kaart. Om dit gemakkelijker te maken, plaatst men vaak een windroos op de kaart.

Deze windroos geeft aan waar het noorden ligt op de kaart. Hiernaast zie je een windroos met de vier hoofd windstreken (noord, oost, zuid, west) en de windrichtingen die daartussen zitten.

Als in de opdracht staat dat je in zuid-oostelijke richting moet lopen, dan ga je dus rechts-schuin naar beneden op de kaart. Moet je naar noord-westelijke richting, dan ga je schuin-links naar boven.

Routes

Er zijn vragen waar je op een kaart uitkomt als je bepaalde instructies hebt gevolgd. Belangrijk hierbij is dat je de windstreken kent zoals boven beschreven. Daarnaast moet je goed in gedachten houden dat wanneer je op de kaart naar beneden gaat je "andersom" moet denken. Dan is rechts ineens links en andersom.

Je ziet dat deze kaart ook een windroos heeft, daardoor kun je je oriënteren op de kaart.

Als ik vanaf de bushalte aan de Bernhardtlaan naar de Wilhelminastraat ga, dan loop ik in zuid-westelijke richting en ga de eerst straat rechts.

Je kan de fout maken dat je linksaf moet, maar je gaat dus naar beneden op de kaart. In dat geval is links rechts, en rechts is dan links!

15.3 Schaal

Op schaal betekent dat iets kleiner of groter is dan in werkelijkheid, denk aan een miniatuur-auto of een souvenir van de Eiffeltoren. De auto hiernaast is ook op schaal. De auto is 24 keer kleiner dan de echte, dat kun je zien aan de verhouding die op de doos staat 1/24. Vaak staat het vermeld als 1:24

1:24 betekent dat 1 cm van deze auto in werkelijkheid 24 cm is.

Werkelijke afstand berekenen.

Op kaarten zie je ook vaak een schaal staan. Het voorbeeld hieronder heeft een schaal van 1 : 45.000

Dat betekent dat 1 cm op de kaart in werkelijkheid 45.000 cm is.

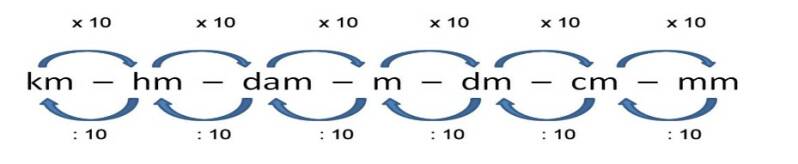
45.000 cm kun je omrekenen naar kilometers. Hiervoor gebruik ik het omrekentabel weer.

45.000 : 100.000 = 0,45

Dus 1 cm op de kaart is in werkelijkheid 0,45 kilometer

De vraag is hoeveel kilometer Mehmet heeft gereden.

Je ziet dat de gemeten afstand op de kaart 10 cm is.

Dus 10 x 0,45 kilometer = 4,5 kilometer.

Ook kun je hier een verhoudingstabel voor gebruiken.

Kijk maar eens hiernaast. Ik heb de gegevens ingevuld die ik weet, startend met de schaal 1 : 45.000

Dan vul ik in wat de afstand op de kaart is, dat is 10 cm.

Op deze wijze kan ik dus de werkelijke afstand uitrekenen: 45.000 : 1 x 10 = 450.000 cm

Nu van centimeters omrekenen naar kilometers: 450.000 : 100.000 = 4,5 kilometer

De schaal berekenen.

Je kunt ook zelf de schaal van een kaart uitrekenen.

Daarvoor moet je de werkelijke afstand weten, en opmeten wat de afstand op de kaart is.

Bij dit voorbeeld zie je dat de gemeten afstand op de kaart 4 cm is.

Onderaan staat dat de werkelijke afstand 100 meter is.

Je berekent de schaal door:

werkelijke afstand in cm : aantal centimeters op de kaart

100 meter = 10.000 cm : 4 cm = 2.500

De schaal is 1 : 2.500

Ook dit kun je oplossen met een verhoudingstabel. Hiervoor moet ik wel zorgen dat ik cm met cm vergelijk, dus als eerste ga ik de meters omrekenen naar centimeters. 100 meter = 10.000 cm

Nu vul ik de gegevens in die ik weet. 4 cm op de kaart is in werkelijkheid 10.000 cm. Ik moet de schaal berekenen, dat betekent dus dat ik terug moet naar 1 cm.

Nu de berekening maken: 10.000: 4 x 1 = 2.500. De schaal is dus 1 : 2.500

Hieronder zie je een video met uitleg over rekenen met schaal.

Toegepast rekenen

Je gaat opgaven tegenkomen waarbij je meerdere berekeningen zal moeten maken. In het voorbeeld hieronder je ook zo'n opgave. Wanneer je naar de opgave kijkt zie je dat er een schaalverdeling te zien is, én dat er in het verhaal erbij gesproken wordt over afstand en tijd. Als dit het geval is moet je weten dat je twee maal een aparte berekening moet maken.

Zoals je ondertussen al wel gemerkt zal hebben, ik ben een groot voorstander van een verhoudingstabel, en ik ga voor deze opgave dan ook twee verhoudingstabellen maken; een om de werkelijke afstand uit te rekenen en een om de km/uur uit te rekenen.

Je gaat opgaven tegenkomen waarbij je meerdere berekeningen zal moeten maken. In het voorbeeld hieronder je ook zo'n opgave. Wanneer je naar de opgave kijkt zie je dat er een schaalverdeling te zien is, én dat er in het verhaal erbij gesproken wordt over afstand en tijd. Als dit het geval is moet je weten dat je twee maal een aparte berekening moet maken.

Zoals je ondertussen al wel gemerkt zal hebben, ik ben een groot voorstander van een verhoudingstabel, en ik ga voor deze opgave dan ook twee verhoudingstabellen maken; een om de werkelijke afstand uit te rekenen en een om de km/uur uit te rekenen.

Op de kaart is te lezen dat de schaal 1 tot 200.000 is. Dat betekent dus dat 1 cm op de kaart in werkelijkheid 200.000 cm is.

De afstand op de kaart is 8 cm (rode lijn). Ik ga nu uitrekenen hoeveel die 8 cm in werkelijkheid is. Daarvoor vul ik het verhoudingstabel in.

1 cm bij schaal en 200.000 bij werkelijk.

Ik moet niet weten wat 1 cm is, maar 8 cm, dus ik moet de schaal x 8 doen. Alles dat ik boven doe, moet ik ook onder doen, dus 200.000 x 8 = 1.600.000 cm

Nu moet ik van cm nog naar km, dus deel ik 1.600.000 door 100.000 en dan kom ik op 16 km.

Nu moet ik nog gaan berekenen hoeveel km/uur Cas rijdt.

Ik weet dat hij 16 kilometer aflegt in 12 minuten. Dit ga ik weer in een verhoudingstabel plaatsen.

Op deze manier kan ik gemakkelijk uitrekenen hoeveel kilometer hij dan in 60 minuten aflegt. Kijk maar hiernaast.

Om van 12 minuten naar 60 minuten (1 uur) te gaan vermenigvuldig ik met 5. Dat moet ik dan ook met de afstand doen. 5 x 16 km = 80 km.

Cas rijdt dus 80 kilometer per uur.