Breuken

Wat zijn breuken?

Een breuk is een deel van het geheel.

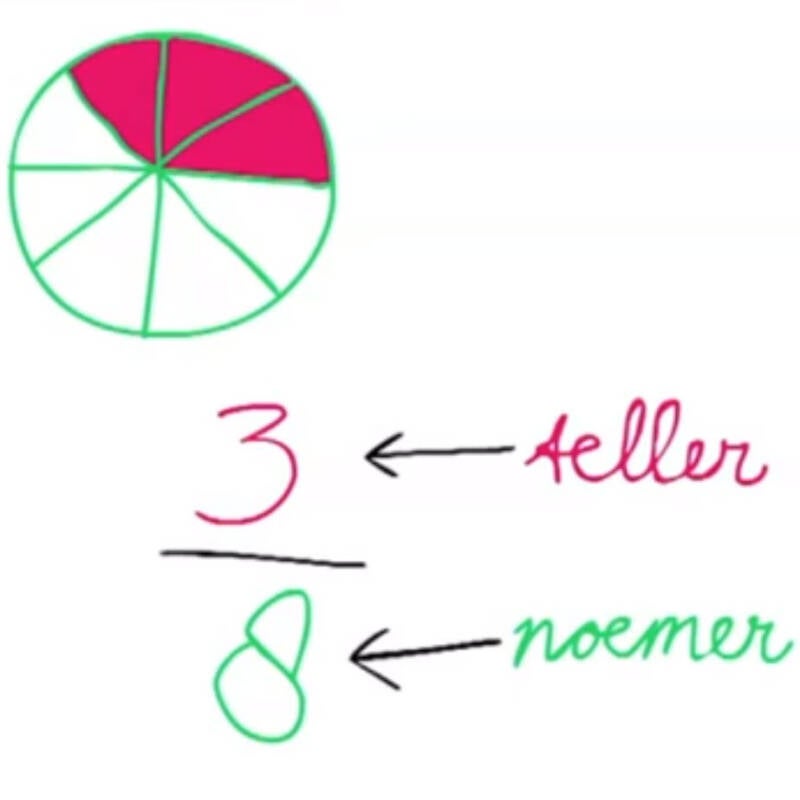
Breuken bestaan uit de teller en de noemer.

De noemer vertelt in hoeveel stukken het geheel is verdeeld, en de teller vertelt hoeveel van deze stukken je gebruikt.

Hieronder is de cirkel in 8 stukken verdeeld, en er zijn er 3 van ingekleurd.

 

Hierboven zie je dat het figuur uit 6 blokken bestaat, dus onder de streep staat 6. En van de zes blokken zijn er 5 blauw. Dus 5/6 van de blokken is blauw.

Breuken op de getallenlijn

Je kan een breuk ook op een getallenlijn plaatsen. Om dat correct te doen moet je kijken in hoeveel stukken de lijn per heel getal is opgedeeld. In het voorbeeld hieronder zie je dat er tussen de 0 en de 1 in totaal zes gelijke stappen genomen kunnen worden. Welke breuk hoort er in het blokje op de getallenlijn hieronder te staan?

 

 

 

 

 

 

 

 

 

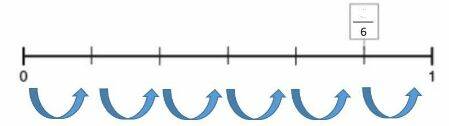
Zoals ik al schreef, de lijn is in zes gelijke delen verdeeld. Dat betekent dus dat onder de noemer (onder de streep) zes moet zijn. 

 

 

Op de hoeveelste stap staat het blokje waar je de breuk moet schrijven? Die staat op het vijfde blokje, van de zes blokjes. Dus de breuk die in het blokje hoort te staan is 5/6

Verschillende soorten breuken, zoek de juiste soort breuk!

Er zijn verschillende soorten breuken. Kijk goed welk met soort breuk je moet werken. Hierbij zijn de noemers erg belangrijk, en uiteraard of je moet optellen of aftrekken, vermenigvuldigen of juist delen. Bekijk je som dus goed, en zoek dan de soort breuk in de uitleggen hieronder. Nogmaals, kijk goed of de noemers gelijk of ongelijk zijn. Succes!

Breuken vereenvoudigen óf juist vergroten.

Breuken moeten je altijd zo ver mogelijk vereenvoudigen. Dat betekent dat je breuken altijd zo klein mogelijk moet maken.

Als je bijvoorbeeld 3/6 hebt, moet je deze zo klein mogelijk maken. Dat doe je door zowel de teller als noemer door hetzelfde getal te delen. In onderstaand voorbeeld kun je beiden delen door 3.

3 : 3 = 1

6 : 3 = 2

3/6 is dus evenveel als 1/2

 

Om het jezelf zo gemakkelijk mogelijk te maken schrijf je de volgende getallen op een blaadje: 2 - 3 - 5 - 7

Als je gaat vereenvoudigen moeten zowel de teller als de noemer door hetzelfde getal deelbaar zijn. Daarvoor gebruik je deze vier getallen. Kijk maar eens naar dit filmpje hieronder.

Wat je zojuist hierboven gedaan  hebt, kan uiteraard ook andersom. Je kan breuken ook vergroten, en wel op dezelfde manier. Dat is met name belangrijk wanneer je straks gaat delen met een breuk.

 

In het filmpje hiernaast worden beide manieren nog eens uitgelegd, dus zowel het vereenvoudigen als het vergroten van de breuken

Belangrijk: noemers MOETEN gelijk zijn of gemaakt worden                             bij optellen en aftrekken met breuken!

Breuken optellen en aftrekken met gelijke noemer

         Beide noemers zijn gelijk

Breuken kun je optellen en aftrekken van elkaar, maar dan moeten ze wel dezelfde noemer hebben!

Hebben ze dezelfde noemer, dan kun je de tellers gewoon van elkaar aftrekken of optellen. De noemer blijft hetzelfde!

2/5 + 1/5 = 3/5

6/9 - 4/9 = 2/9

 

Breuken optellen en aftrekken met ongelijke noemer,

maar in dezelfde tafel.

Moet je een breuk optellen of aftrekken met een verschillende noemer, dan moet je eerst de noemers gelijk maken.

Dat kan op twee manieren: 

          Beide noemers in de tafel van 3

1. Je kunt de noemer gemakkelijk aanpassen door verdubbelen of delen. Bijvoorbeeld: 1/3 + 1/6

    We hebben hier derden en zesden als noemers.

 Bij het vereenvoudigen zag je dat je breuken kunt vereenvoudigen, maar dan dus ook vermeerderen. Dat heb ik boven ook al uitgelegd. Daar staat ook een filmpje bij. Kijk maar eens:

 

Hierboven hebben we dus 1/3 omgerekend naar 2/6.

Nu is dus de som veranderd naar 2/6 + 1/6

2/6 + 1/6 = 3/6 

En 3/6 moeten we weer vereenvoudigen naar 1/2

Breuken optellen en aftrekken met ongelijke noemer,

en niet in dezelfde tafel.

      12 is hier de gedeelde noemer

3 x 4 = 12 

2. Kun je de ene noemer niet aanpassen aan de andere, dan moet je de       volgende strategie toepassen.

   Als voorbeeld hebben we de volgende som:

   2/3 + 1/4

 Je ziet dat de noemers ongelijk zijn. Hoe gaan we ze dan gelijknamig maken? 

 Hiervoor moeten we drie keer een "keer-som" maken, de som opnieuw     opschrijven, en het mooiste van alles, we gaan een vlinder tekenen

  Hieronder zie je hoe je dat moet doen.

Hier een video met uitleg over het optellen en aftrekken van breuken met de zogenaamde 'vlinder-methode'.

Breuken vermenigvuldigen 

Bij het vermenigvuldigen van breuken 'steek je recht over'.

Daarmee bedoel ik dat je de teller x de teller doet, en de noemer x de noemer.

Breuk vermenigvuldigen met een heel getal, of andersom

Wanneer je een breuk gaat vermenigvuldigen met een heel getal, dan ga je alleen de teller vermenigvuldigen met het hele getal.

4 x 1/6 =

4 x 1 = 4

 

De noemer blijft hetzelfde. Het juiste antwoord is dus 4/6

Deze weer vereenvoudigen, en dan krijg je 2/3

3 x 1/4 =

3 x 1 = 3

De noemer blijft hetzelfde, dus 3/4 is het antwoord.

Hieronder zie je een video met uitleg.

Breuken delen = vermenigvuldigen met het omgekeerde

Om breuken te kunnen delen werken we met het volgende:  "Delen is vermenigvuldigen met het omgekeerde".

Ik ga je niet uitleggen waarom, maar het werkt wel.

Kijk naar de volgende som: 

We gaan deze oplossen met het principe: "Delen = vermenigvuldigen met het omgekeerde".

Dat betekent dat we het : vervangen door x, en we draaien de achterste breuk om. 

Kijk maar naar het voorbeeld hieronder.

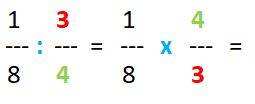
De regel bij vermenigvuldigen van breuken is recht oversteken, dus:

teller x teller en noemer x noemer.

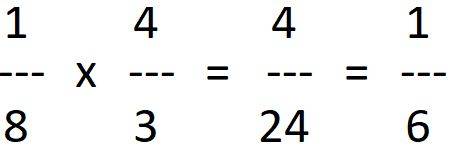
Om het wat duidelijker te maken heb ik een video toegevoegd.

Mochten breuken je hierna nog steeds niet helder zijn, neem dan eens een kijkje op deze website. Daar worden álle soorten breuken nogmaals uitgelegd met heldere video's.

Breuken en decimale getallen

 

Breuken en decimale getallen, daar krijg je hier uitleg over.

Belangrijk hierbij is dat je weet hoe je een decimaal getal uitspreekt. Bijvoorbeeld 1/10 spreek je uit als één-tiende. Als je weet hoe het schema hiernaast werkt, dan weet je direct dat je het als 0,1 schrijft.

 

Hieronder zie je een filmpje waarin het wordt uitgelegd.

Maak jouw eigen website met JouwWeb