Lijnen en figuren

Overal om je heen kom je ze tegen, lijnen en figuren. Maar ook symmetrie of juist asymmetrie zie in het dagelijks leven. Deze benamingen komen je vast en zeker bekend voor, maar weet je ook nog wat een prisma is, of een kegel? En wat was ook alweer verticaal? Al dit soort zaken komen hier aan bod.

Horizontaal en verticaal

Voor het rekenen op 2f niveau moet je het verschil weten tussen bovenstaande benamingen, horizontaal en verticaal. Hieronder zie je ze afgebeeld. Links zie je horizontaal, denk daarbij aan de boot aan de horizon. De horizon is dus plat, van links naar rechts (of andersom).

Verticaal is het tegenovergestelde, namelijk van boven naar beneden (of andersom), denk aan de raket die de lucht in gaat.

Evenwijdige lijnen

Evenwijdige lijnen wil zeggen dat de ruimt tussen de lijnen hetzelfde is, en hetzelfde blijft. Ook al kijk je 1.000 kilometer verder, ze lopen nog steeds evenwijdig. Deze lijnen zullen elkaar dus nóóit kruizen. 

Haakse of rechte hoek

Links zie je een  winkelhaak, die metalen liniaal. Deze wordt in de bouw gebruikt om ramen, muren en deuren perfect recht te kunnen plaatsen. Ze noemen dat ook wel "haaks" geplaatst. 

 

De hoeken die je ziet op de winkelhaak, maar ook bij de groene figuur zijn perfect haaks. Je kunt dit ook een rechte hoek noemen, 

 

De twee lijnen in de groene figuur staan loodrecht tegenover elkaar. Dat betekent dat ze perfect haaks tegenover elkaar staan. 

 

Men spreekt hier ook wel over een hoek van 90 graden (90°).

Tweedimensionale vormen (2D)

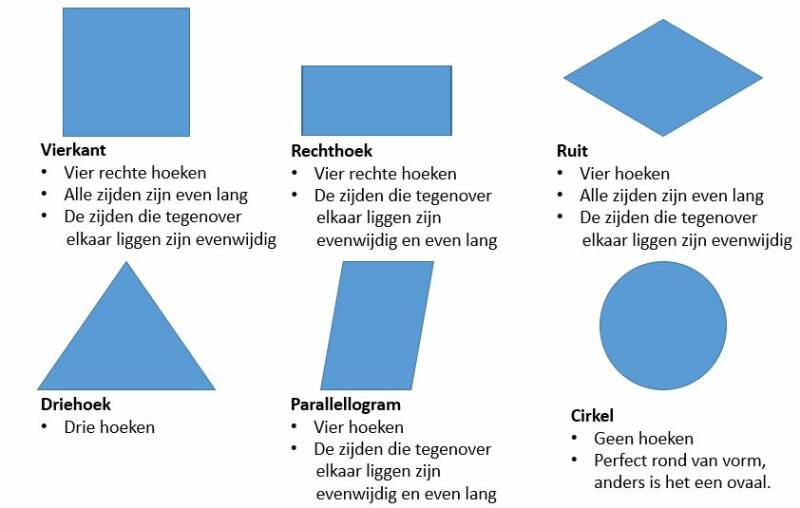
Hieronder zie je zes verschillende tweedimensionale vormen. Tweedimensionaal wil zeggen dat het "platte" figuren zijn, dus ze hebben geen diepte. Eigenlijk hebben ze alleen een lengte en een hoogte

De cirkel

Over de cirkel moet ik je nog wat meer vertellen. Deze heeft namelijk een afwijkende vorm, hij heeft geen hoeken. Normaal ga je de lengtes tussen hoek opmeten om te kunnen berekenen hoeveel er in iets past of hoe lang iets is. Dát werkt net even anders bij een cirkel. Dat ga ik je hier uitleggen.

Een cirkel heeft een middelpunt. Dat is letterlijk het midden van een cirkel. (geel)

 

Een cirkel heeft een omtrek. Die kun je bereken door een touwtje om de cirkel te leggen en de afstand dan op een liniaal af te lezen. (rood)

 

Een cirkel heeft een straal. Dat is vanaf het middelpunt gemeten tot aan de rand van de cirkel. (oranje)

 

Een cirkel heeft een diameter. Dat is de de totale breedte van een cirkel. Aangezien een cirkel perfect rond is, is de diameter op elk punt gelijk. De diameter is twee keer de straal. (grijs)

Driedimensionale vormen (3D)

Naast de tweedimensionale vormen bestaan er ook driedimensionale vormen. Deze hebben ook nog diepte. Ze hebben dus naast lengte en breedte ook diepte, dus drie dimensies.

Hieronder zie je enkele vormen met drie dimensies.

Uitslagen

En hier bedoel ik geen uitslag onder je voeten of de voetbaluitslagen. Nee, ik bedoel hiermee de uitslagen van bovenstaande 3d figuren.Denk daarbij aan een bouwplaat die je zelf moet uitknippen, zodat je deze in elkaar kunt zetten tot bijvoorbeeld een kubus,

 

In het filmpje hiernaast filmpje wordt het een en ander uitgelegd over dit onderwerp. Er wordt ook over "ribben" gesproken, maar dat hoef je niet te weten.

Ik wil je alleen een inzicht geven welke vormen er zijn, en hoe de bijbehorende uitslagen er uitzien.

 

Als je naar de uitslagen hiernaast kijkt, van welke van deze uitslagen kun je een kubus maken?

 

 

Juist, dat lukt met uitslag C. Uitslag A maakt een balk en uitslag B zal tot een kubus leiden.

 

 

Symmetrie

Symmetrie is een afbeelding dat in twee helften verdeeld kan worden en die dan precies of ongeveer spiegelbeeldig zijn. Het tegenovergestelde is asymmetrie. Ik kan hier veel woorden over vuil maken, maar ik denk dat onderstaande afbeelding voldoende zegt.

Aanzichten

Van welke kant bekijk je een figuur, of welke figuur zie je hier? Men zou ook nog kunnen vragen uit hoeveel blokjes een figuur bestaat. Zomaar drie vragen die van toepassing zijn op dit onderdeel. Hierbij moet je even goed nadenken en een scherp oog hebben.

 

De video hiernaast geeft je uitleg over deze lesstof.

Kijklijnen

Tot slot nog het onderdeel kijklijnen. Denk hierbij aan de vraag: op welk punt in de tekening sta ik wanneer ik het standbeeld zie?

 

Je ziet hiernaast een afbeelding van bovenaf. In het midden staat een standbeeld een boom en vier flatgebouwen. 

Daarnaast zie je een A, B, c en D. 

Vraag: Bij welke letter sta ik wanneer ik het beeld kan zien?

In het filmpje hieronder wordt het een en ander uitgelegd.             

Wanneer ik de kijklijnen heb getekend, zie je dat ik bij punt B het standbeeld kan zien. Vanaf de andere punten staan de gebouwen in de weg.