
Procenten
Procent betekent letterlijk per honderd (1 van de honderd, dus één-honderdste). Je kunt dit ook schrijven als een breuk 1/100. Dit is ook al eerder bij het hoofdstuk Breuken beschreven.
Wanneer je alles hebt, dan heb je 100 van de 100, dus 100%.
Heb je 50%, dus de helft, dan heb je 50/100. (5/10 = 1/2)
Zoals je ziet, ook hier komen de breuken weer tevoorschijn.
Voor het rekenen met procenten is het verhoudingstabel ideaal. Zoals ik al eerder schreef maak ik gebruik van het verkorte verhoudingstabel, dat werkt lekker snel.
Voor uitleg hierover kijk je even naar het hoofdstuk "Het verhoudingstabel" in het bovenste menu.
Aan de onderzijde van deze pagina zie je uitgewerkte opgaven in de filmpjes.

Procenten: verschillende soorten sommen
Wat het berekenen van procenten vaak lastig maakt, is dat er zoveel verschillende soorten opgaven lijken te zijn. Maar eigenlijk zijn alle opgaven terug te brengen tot 5 soorten:
- Sommen waarbij je een deel in procenten, of juist in aantallen moet uitrekenen;
- Sommen waarbij je het deel weet en je het geheel (100%) moet uitrekenen;
- Sommen waarbij je het nieuwe totaal moet uitrekenen.
- Sommen waarbij je de stijging of daling in procenten moet uitrekenen.
- Sommen waarbij je het oude totaal moet uitrekenen.
Deze vijf soort sommen ga ik je hier onder, en het volgende hoofdstuk uitleggen, maar eerst nog even verder met de uitleg wat procenten precies zijn, en wat ze met de breuken, verhoudingen en de decimale getallen te maken hebben.
Wat zijn procenten?
Zoals ik hierboven al schreef, procent betekent per honderd/
Ik zal het uitleggen met behulp van een paar afbeeldingen.
Hiernaast zie steeds een vierkant die uit 100 blokjes bestaat. Bij elk vierkant is steeds een ander aantal blokjes geel gekleurd.
Omdat het steeds 100 blokjes zijn en een deel is hiervan gekleurd spreken we over een deel per honderd, dus procent.
Wanneer er 14 blokjes van de honderd geel zijn gekleurd, zijn het er dus 14 per honderd, en dat is dus 14 procent (%)
Zouden alle blokjes ingekleurd zijn, dus 100 van de 100, dan spreek je over 100%
Alles = 100%

Procenten, breuken, verhoudingen en decimale getallen
Zo hey, dat is een mond vol zeg!
Bovenstaande hebben álles met elkaar te maken, ze geven allemaal aan dat iets ergens een deel van is. Dat kan dus door middel van een percentage (10%), een breuk (1/10), een verhouding (1:10) of een decimaal getal (0,10)
Er wordt van je verwacht dat je deze allemaal kunt inzetten en met elkaar kunt verwerken, dus van een breuk naar een decimaal getal kunt rekenen, of van een percentage naar een breuk kunt omrekenen.
Hiernaast zie je een filmpje die uitlegt hoe procenten en breuken en decimale getallen met elkaar te maken hebben.
Van breuk naar procenten.
Op school hebben van alle studenten 3 op de 10 bruin haar.
Vraag: hoeveel procent van alle studenten op school hebben bruin haar?
Hiernaast zie je de uitwerking hiervan.
We moeten 3/10 omrekenen naar 100. 3/10 = 30/100 = 30%
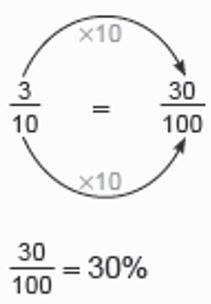
Daarnaast kunnen we deze som ook nog oplossen met behulp van het verhoudingstabel. Kijk hieronder maar eens.

Je ziet, zolang ik maar noteer waar het over gaat (deel en totaal in dit geval), kan het eigenlijk niet fout gaan met rekenen. Ik moet weer rekenen naar de 100 bij de noemer (totaal)
En nu andersom, van procenten naar een breuk.
De chocoladereep bestaat voor 80% pure cacao.
Vraag: Welke breuk hoort daarbij?
Zoals je ziet; 80% = 80/100
De regel bij breuken: altijd vereenvoudigen, dus zo klein mogelijk maken!
80/100 = 8/10 = 4/5


En nu nog van percentage naar een decimaal getal.
Ik hanteer dit ezelsbruggetje altijd bij de uitleg hiervan: proCENT.
Denk bij kommagetallen altijd aan geld, want met geld reken werkt gemakkelijker.
Neem 65% als voorbeeld. Denk nu aan 65 (pro)CENT, hoe schrijf je dat, 65 cent?
Precies: €0,65 Dus 65% = 0,65
Officieel maak je deze berekening: 65 : 100 = 0,65

Rekenen met procenten
Belangrijk hierbij is echt goed lezen wat er in de opgave vermeld staat, en waar moet je die gegevens in het tabel plaatsen.
Een deel van het totaal uitrekenen
Je rekent dan met percentage en het totaal uit hoe groot een deel is.
We gaan nu een deel van een geheel uitrekenen.
Een straat heeft 25 huizen. (Alle huizen samen is 100%). Van deze huizen heeft 28% een rode deur.
Hoeveel huizen hebben een rode deur?
Maak een verhoudingstabel, en vul de gegevens in die je weet.
Onthoud dat alle huizen samen 100% is.
Er wordt gevraagd hoeveel deuren er rood zijn, dus 28% van 25.
Zoals je ziet, er zijn 7 huizen die een rode deur hebben.

Je kunt op dezelfde wijze ook het percentage uitrekenen.
Er zijn 80 verpleegkundigen aan het werk bij het verzorgingstehuis. Hiervan zijn er 18 boven de 50 jaar oud.
Hoeveel procent van de verpleegkundigen zijn boven de 50 jaar oud?
Als je het juist hebt ingevuld en uitgerekend kom je uit op 22,5%

Het totaal (100%) uitrekenen.
Hier moet je goed kijken waar je welke cijfers neerzet. In onderstaand voorbeeld moet je terugrekenen naar 100%, deze komt dus in de achterste rij te staan. Kijk maar eens.

Je batterij van de telefoon zit nog voor 45% vol en je kunt hem nog 495 minuten gebruiken.
Hoeveel minuten gaat een volle batterij mee?
Kijk goed hoe je het tabel nu moet invullen! Ik moet naar de 100% toe.
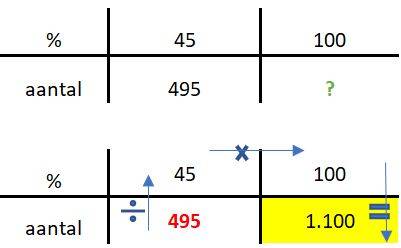
Je ziet dat je een goed overzicht krijgt wanneer je een verhoudingstabel gebruikt.
Met een volle batterij (100%) kun je 1.100 minuten gebruik maken van de telefoon.
Toegepast rekenen met procenten.
In 2019 kwamen er 24.000 bezoekers naar het Festival X waarvan een derde uit het buitenland kwam.
Van het aantal buitenlands bezoekers kwam 12% uit Polen.
Vraag: hoeveel Poolse bezoekers kwamen er dat jaar naar Festival X?
Als je goed hebt gelezen zie je dat 1/3 van 24.000 uit het buitenland kwam. Van dat aantal bezoekers kwam 12% uit Polen. Hier moet ik dus 2 tabellen maken.



Er kwamen dus 8.000 bezoekers uit het buitenland.
Nu moet ik nog uitrekenen hoeveel 12% van 8.000 is.
Om dat uit te rekenen maak ik opnieuw een tabel. Belangrijk daarbij is dat het totaal aantal buitenlandse bezoekers 8.000 is, dat is dus 100%.


Zoals je hiernaast kunt zien kwamen in 2019 960 bezoekers uit Polen.
Hoeveel vrachtauto's werden er uiteindelijk gecontroleerd?


Ook hier geldt weer; erg goed lezen. Wat staat nu exact in het krantenknipsel vermeld?
Als je het goed hebt gelezen zie je dat er 1.330 vrachtwagens een gevaar op de weg waren, en dat was 14% van alle gecontroleerde vrachtwagens. We moeten dus uitrekenen hoeveel 100% is, want dat is het totaal aantal gecontroleerde vrachtwagens. IK maak weer een tabel, en zorg dat ik de juiste getallen op de juiste plek plaats.

Hiernaast zie je dus dat er 9.500 vrachtauto's zijn gecontroleerd.

Hier een video waar het rekenen met procenten wordt uitgelegd.
- Home
- Optellen en aftrekken
- Vermenigvuldigen, delen en rekenregels
- Decimalen
- Breuken
- Toegepast Rekenen
- Het verhoudingstabel
- Verhoudingen
- Verhoudingen en breuken
- Procenten
- Procentuele afname en toename
- Lijnen en figuren
- Maten en hoeveelheden
- Omtrek
- Metriek Stelsel
- Oppervlakte
- Inhoud
- Tijd, snelheid en afstand
- Kaart en schaal
- Tabellen en Schema's
- Diagrammen
- Verbanden en formules
- Oefenexamens
- Weten
- Reacties
- Hulpkaarten

